Calculating Vega in Your Head
30 Nov 2019

TL;DR

Derivation

Black Scholes for a Call/Put option is

It’s easy to see

With ATMF strike, ,

Here comes the approximation part, for short expiries and a wide range of vols,

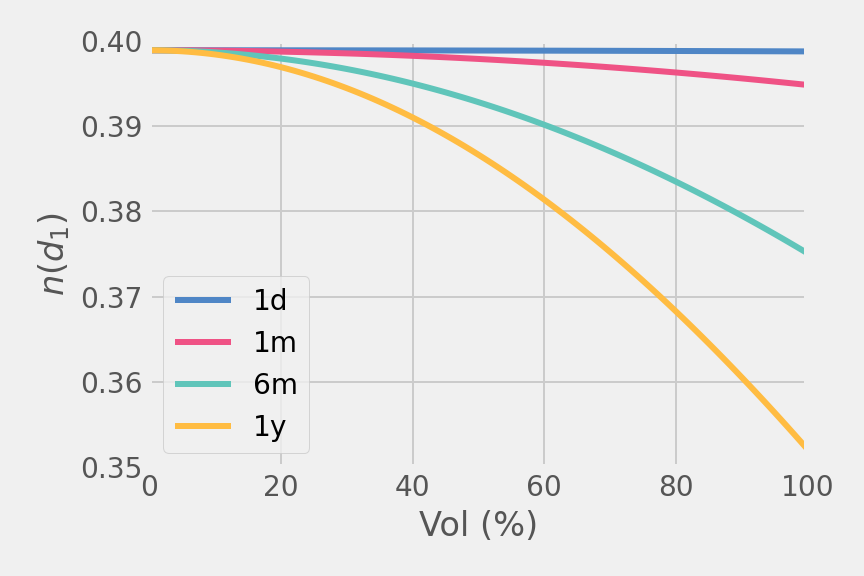
It’s easier to check this plot of against volatility for different expiries. Immediately we see that even in an extreme market with 100% vol, the approximation is largely correct for short expiries.

$$n(d_1) vs Volatility$$

Shortcut

Recall that we derived the approximation of ATM option price in Calculating Option Price in Your Head,

immediately you have vega

In Practice

We notice that ATM volatility does not have a strong impact on ATM Vega, this is expecially true for short-dated options.

In Forex, vega are often quoted in asset bps for 1% vol move. Above approximation intepreted in such a style is

Junior traders often find the below table of approximated vega for standard expiries helpful.

Expiry	1d	1w	2w	1m	2m	3m	6m	9m	1y
Vega (asset bps)	2.09	5.52	7.81	11.63	16.31	20.03	28.17	34.57	39.89

Exercise

Q: What is the vega amount for a 100 mio notional USDJPY 1m ATM option?

A: From above table we know the vega in asset bps is 11.63, thus total vega in USD is

The vega amount is 116.3 K USD.